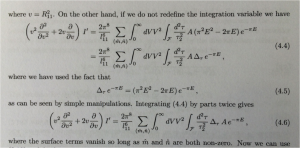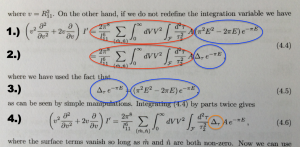Eine der Basistechniken für schnelles Lesen ist das sog. „Chunking“: das Bündeln von Wörtern zu Sinngruppen anstelle von Einzelwortlesen – womit gleichermaßen Lesetempo und Leseverständnis erhöht werden:

Als ich vergangene Woche ein Improved Reading-Training bei einem Potsdamer Max-Planck-Institut gegeben habe, reichten mir die Teilnehmer wie üblich einige Beispiele aus ihrer alltäglichen Lesepraxis ein. Da es sich um Physiker und Mathematiker handelte, sah das dann z.B. so aus:

Obwohl ich kein Mathematiker bin, war ich doch neugierig auf diese Textart und fragte mich (und die Teilnehmer), inwiefern Speed Reading wohl auch hier anwendbar sei.

Chunking-Technik auch bei mathematischen Formeln nützlich

Naheliegend war für alle, dass die „Klartext-Passagen“ zumindest teilweise mit derselben Chunking-Technik gelesen werden können wie andere Texte auch – das nötige Vorwissen und die Automatisierung des fachlichen Wortschatzes vorausgesetzt. Aber wie sieht es bei den Formeln und Gleichungen aus? Auch ohne den Text inhaltlich verstehen zu können, stieß ich auf die folgende Passage, an der ich einige Parallelen zu unserem Ansatz verdeutlichen konnte:

Was sofort auffällt, sind die Klammern und Integralzeichen als bereits vorhandene Begrenzungen für „mathematische Sinngruppen“. Die folgende Grafik zeigt, wie sich die Formeln auf einer rein „formalen“ Ebene, also ohne inhaltliches Verständnis, mithilfe der Chunking-Technik weiter analysieren lassen:

Aus dem Vergleich von Zeile 1.) und 2.) ergibt sich, dass beide Zeilen rechts des Gleichheitszeichens offensichtlich denselben Wert haben – und auf den ersten Blick auch recht ähnlich aussehen, allerdings unterschiedlich lang sind. Irgendwo müssen sie sich also unterscheiden. Bei näherem Hinsehen stellt sich heraus, dass die rot eingekreisten Bereiche komplett identisch sind und sich nur die Inhalte der blauen Kreise rechts daneben unterscheiden. Folgerichtig erscheinen diese in Zeile 3.) als eigenständige Gleichung.

Was hat das mit Chunken zu tun? Nun, genauso wie ein erwachsener Leser nicht jedes Wort einzeln lesen sollte, sondern Wortgruppen als Ganzes erfasst, wird auch ein geübter Mathematiker die Zeichen nicht einzeln nacheinander dechiffrieren, sondern größere Bereiche gleichzeitig erfassen. Wenn ihm die Zeichen und Formeln genügend vertraut sind, lässt sich dieser Bereich – im Rahmen der optisch möglichen Blickspanne von ca. 3,5 cm – ähnlich ausweiten wie das beim Lesen der Fall ist.

Auf diese Weise lassen sich Ähnlichkeiten und Unterschiede bei solchen Gleichungen sehr viel schneller erfassen. Das zeigt sich auch in Zeile 4.), deren rechte Hälfte fast identisch ist mit Zeile 2.) – der Unterschied besteht allein in der Position des orange eingekreisten Delta-Symbols.

Viele Speed Reading-Techniken einsetzbar

Weitere Techniken aus dem „Speed Reading-Handwerkskasten“, die auch bei solchen Texten hilfreich sein könnten, sind z.B. das „Scannen“ (fokussierende Suche) nach gezielten Suchbegriffen (oder -symbolen) mithilfe vorheriger Visualisierung und natürlich die vorherige Vorausschau, mit der ein Überblick über den Text gewonnen wird.

In der Diskussion mit den teilnehmenden Doktoranden und Post-Docs wurde mir vor allem eins bewusst: dass es auch bei hochkomplexen mathematischen Texten nicht von vorne herein und manchmal überhaupt nicht darauf ankommt, jedes Detail, jedes Zeichen für sich zu verstehen, sondern die logischen Strukturen nachzuvollziehen. Und diese sind erst aus dem Zusammenhang erkennbar, der sich seinerseits aus dem Bündeln der Einzelinformationen und dem Überblick aufs Ganze ergibt. (Die enge „Schlüsselloch-Perspektive“ verstellt eher den Sinn fürs Wesentliche.)

Voraussetzung dafür ist, wie bei den philosophischen Texten, mit denen ich aus meiner Ausbildung vertraut bin, ein mehrstufiges Vorgehen – also eine Kombination aus Vorausschau, Chunken, Scannen und anderen Techniken. Und gerade nicht der Anspruch, alles beim ersten (ganz langsamen) Lesen verstehen zu „müssen“.